Prediction in ISS

Prediction plays a pivotal role in autonomous driving, determining the probable actions of on-road agents to ensure safe navigation. In this documentation, we outline our current methodologies, from the simple constant velocity motion predictor to the more advanced Motion Transformer, including specific methodologies for pedestrian trajectory prediction.

Constant Velocity Motion Predictor

Overview

The constant velocity model is the most basic but effective method of prediction¹, assuming an entity continues its current trajectory at a constant speed. Here, we forward simulate the kinematic bicycle model via the Runge-Kutta 4 (RK4) integration, assuming no variation in acceleration and steering angle.

Applicability and Limitations

• Applicability: ideal for high-speed highways where motion is relatively linear.
• Limitations: in urban or crowded areas, this model may not capture erratic movements of the agents.

Mathematical Model

Kinematic bicycle model

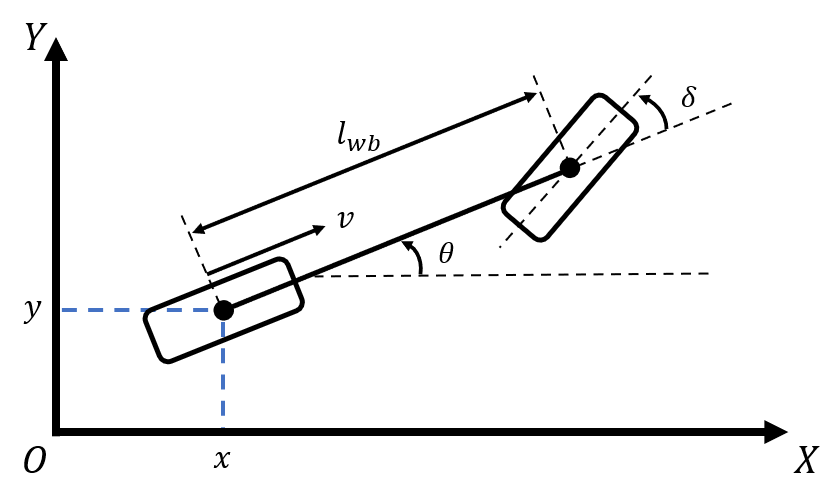
The primary equations governing the kinematic bicycle model are:

1. Position updates: the spatial coordinates of the vehicle rear wheel are updated from time $t$ to time $t + 1$ as

   $$x(t+1) = x(t) + v(t) \cos(\theta(t)) \Delta t$$ $$y(t+1) = y(t) + v(t) \sin(\theta(t)) \Delta t$$

2. Heading update: the heading of the bicycle changes as

   $$\theta(t+1) = \theta(t) + \frac{v(t)}{l_{wb}} \tan(\delta) \Delta t$$

where

• $(x, y)$ represents the vehicle’s position;
• $\theta$ is the vehicle’s heading;
• $v$ denotes the vehicle’s velocity;
• $\delta$ is the steering angle at the front wheel;
• $l_{wb}$ is the wheelbase, i.e., the distance between the front and rear axles; and
• $\Delta t$ is the time step.

The RK4 method is then applied for forward simulation to improve prediction accuracy over short horizons.

Sample Use Cases

• Highways and expressways.
• Open areas with minimal obstructions.

In ISS, the constant velocity model is incorporated for motion forecasting in the structured road environment.

Motion Transformer

Overview

The Motion Transformer² is a state-of-the-art model that considers historical data to predict future trajectories. This framework models the motion prediction as a joint optimization of global intention localization and local movement refinement. Apart from considering the global information of the road structures, this method also incorporates different motion modes by adapting learnable motion queries. The overall structure of the Motion Transformer is shown in the figure below.

The structure of the motion transformer

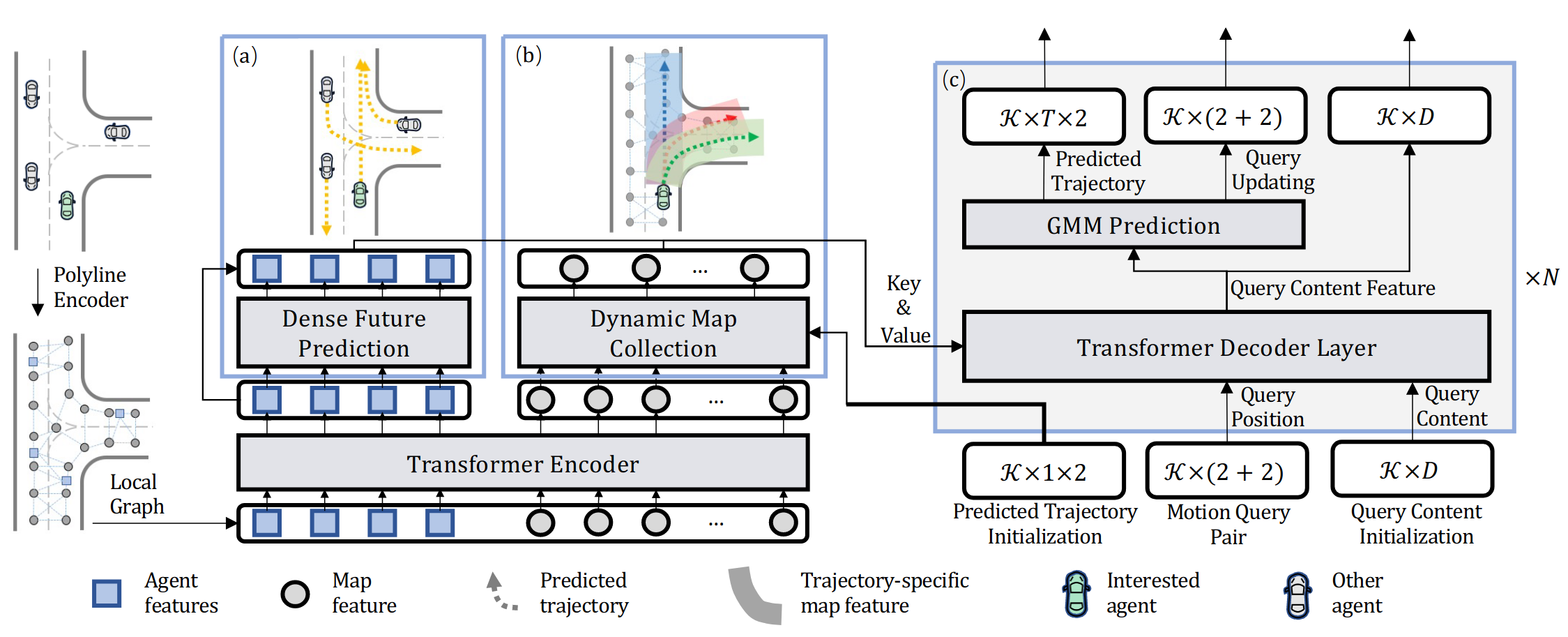
Why Motion Transformer?

Simpler models lack the nuance needed for complex environments. The Motion Transformer accounts for historical trajectories, giving it an edge in intricate scenarios.

Architecture & Components

• Attention Mechanisms: to weigh the importance of different historical data points.
• Encoder-Decoder Structures: the encoder processes the input sequence, while the decoder produces the predicted trajectory.

Input/Output Details

• Input: historical trajectory data.
• Output: predicted future trajectories with confidence intervals.

Pedestrian Trajectory Prediction

About Pedestrian Trajectory Prediction

Pedestrian trajectory prediction involves forecasting the future movements of pedestrians within a given environment. In the context of autonomous driving, accurately predicting where pedestrians will move is crucial for the safety and efficiency of self-driving vehicles.

Input/Output Details

• Input:
  • Historical trajectories: the past positions of pedestrians over a certain time window.
  • Scene Context (optional): information about the environment, such as maps, road layouts, and static obstacles.
  • Agent Interactions (optional): data on the movements of other nearby agents, including vehicles, cyclists and so on.
• Output:
  • Predicted trajectories: estimates of future pedestrian positions over a specified prediction horizon.
  • Probability distributions (in probabilistic models): representations of the uncertainty associated with each predicted trajectory.

Classic Trajectory Prediction Models

Below, we highlight four models that have notably contributed to research and development in pedestrian trajectory prediction.

Trajectron++³ is a graph-structured recurrent model designed for multi-agent trajectory prediction. It represents agents and their interactions using a dynamic spatiotemporal graph, allowing the model to capture the complex dependencies between multiple pedestrians and vehicles. Trajectron++ effectively handles varying agent quantities and can predict multiple socially acceptable future trajectories for each agent.

AgentFormer⁴ introduces a transformer-based architecture to model the temporal and social dimensions of trajectory prediction. By leveraging attention mechanisms, AgentFormer can capture long-range dependencies in both time and space. This model excels in scenarios with dense traffic, where understanding the interactions between many agents is critical for accurate prediction.

MID⁵ formulates trajectory prediction with motion indeterminacy diffusion. In the framework, it learns a parameterized Markov chain conditioned on the observed trajectories to gradually discard the indeterminacy from ambiguous areas to acceptable trajectories. By adjusting the length of the chain, it achieves the trade-off between diversity and determinacy.

MemoNet⁶ employs a memory network architecture to enhance trajectory prediction. It stores representative instances in the training set and recalls them during prediction, providing a more explicit link between the current situation and the seen instances. This approach helps in scenarios where pedestrian behavior is influenced by habitual patterns or when the environment has repeating structures.

The main details about the above models are summarized in the following table:

Model	Trajectory prediction type	Input	Output	Algorithms
Trajectron++	Pedestrian/Vehicle	Past trajectories Dynamic and static context information	Future trajectories (multimodel)	Graph-structured recurrent neural network CVAE
AgentFormer	Pedestrian/Vehicle	Past trajectories	Future trajectories (multimodel)	Spatio-temporal dependencies model CVAE
MID	Pedestrian	Past trajectories	Future trajectories (multimodel)	Diffusion probabilistic model Transformer-based
MemoNet	Pedestrian	Past trajectories	Future trajectories (multimodel)	Memory network architecture Transformer-based

Robustness Verification in Pedestrian Trajectory Prediction

Although current methods for predicting human trajectory have achieved remarkable results, they still face security risks due to their susceptibility to adversarial attacks. As pedestrian trajectory prediction models are deployed in real-world autonomous systems, ensuring their robustness becomes essential.

References

1. Schöller C, Aravantinos V, Lay F, et al. What the constant velocity model can teach us about pedestrian motion prediction. IEEE Robotics and Automation Letters, 2020, 5(2): 1696-1703. ↩

2. Shi S, Jiang L, Dai D, et al. Motion transformer with global intention localization and local movement refinement. Advances in Neural Information Processing Systems, 2022, 35: 6531-6543. ↩

3. Salzmann T, Ivanovic B, Chakravarty P, et al. Trajectron++: Dynamically-feasible trajectory forecasting with heterogeneous data. 16th European Conference in Computer Vision (ECCV). Springer, 2020, XVIII 16: 683–700. ↩

4. Yuan Y, Weng X, Ou Y, et al. Agentformer: Agent-aware transformers for socio-temporal multi-agent forecasting. IEEE/CVF International Conference on Computer Vision. IEEE, 2021: 9813–9823. ↩

5. Gu T, Chen G, Li J, et al. Stochastic trajectory prediction via motion indeterminacy diffusion. IEEE/CVF Conference on Computer Vision and Pattern Recognition. IEEE, 2022: 17113–17122. ↩

6. Xu C, Mao W, Zhang W, et al. Remember intentions: retrospective-memory-based trajectory prediction. IEEE/CVF Conference on Computer Vision and Pattern Recognition. IEEE, 2022: 6488–6497. ↩