Verification by Formal Methods
Motivation
Formal verification methods provide a mathematically sound approach to ensure the correctness, safety, and reliability of systems. Unlike traditional testing methods, formal methods aim to prove properties about a system using logical reasoning, which is especially important for systems where failure can have catastrophic consequences, like autonomous driving. Formal verification techniques, including automata learning, probabilistic model checking, and hybrid system analysis, offer powerful tools for ensuring that complex systems adhere to desired safety and performance criteria.
Verification Frameworks
The following formal verification frameworks are commonly used to ensure the safety, reliability, and correctness of AI systems:
-
Automata learning
Automata learning is a technique used to automatically infer finite-state models (automata) of systems based on observed behavior or interactions. This approach is particularly useful for learning the behavior of black-box systems, such as deep learning models, and helps identify and verify safety-critical properties by generating a formal model that can be analyzed. By inferring a model of the system’s behavior, automata learning enables rigorous analysis of system dynamics and safety properties.
-
Probabilistic model checking
Probabilistic model checking extends classical model checking to handle systems with probabilistic behavior, such as stochastic processes or systems with inherent uncertainty. This technique allows the verification of properties expressed in probabilistic temporal logic, such as ensuring that a system has a high probability of reaching a safe state. Probabilistic model checking is particularly useful for analyzing AI systems with stochastic components, such as reinforcement learning agents or systems operating in uncertain environments.
-
Hybrid system analysis
Hybrid systems combine both discrete and continuous dynamics, which is common in real-world systems controlled by AI. Hybrid system analysis involves the verification of both the continuous behavior of the system (such as its physical dynamics) and the discrete behavior (such as logic or decision-making processes). Techniques like reachability analysis and reach-avoid are applied to hybrid systems to ensure that they meet safety and performance requirements under all possible conditions.
Techniques
The following techniques are commonly used in our tools.
- Automata learning
- LTL to automata translation
- Reach-avoid analysis
- PAC learning
- Scenario approach
Tools
We have also developed tools for automata learning, probabilistic model checking and verifying hybrid systems:
- ROLL
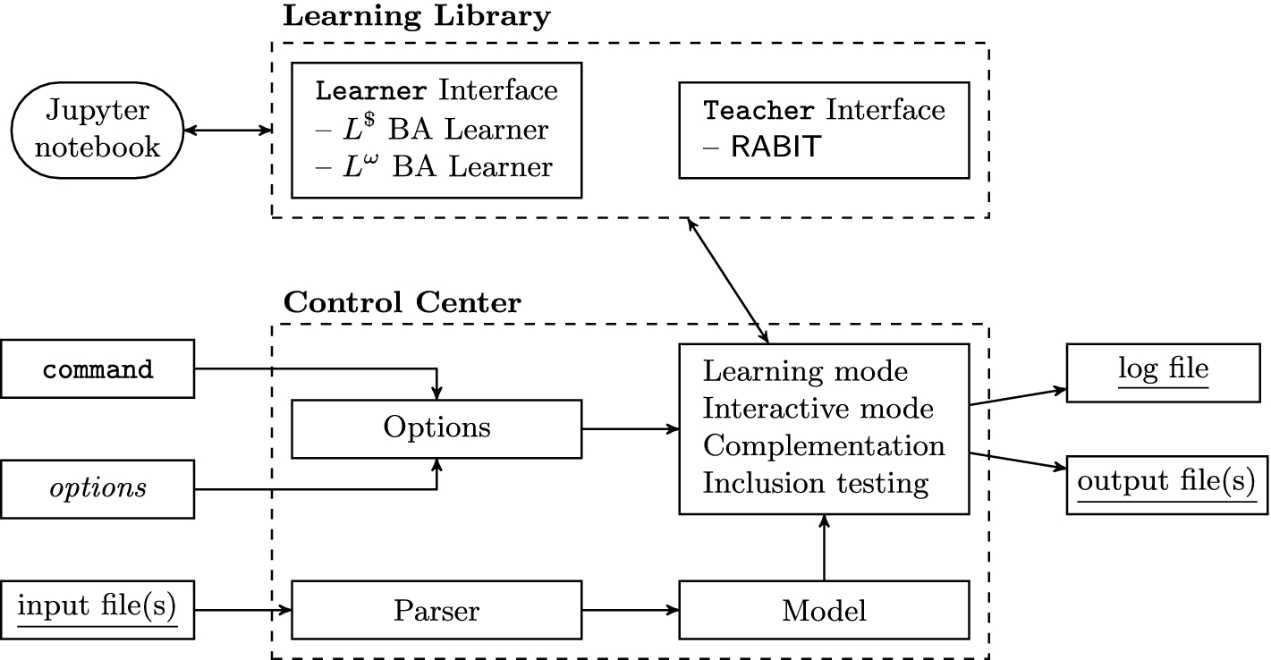
ROLL is an open source learning library for omega-regular languages, including automata models like nondeterministic Büchi automata, deterministic Büchi automata, limit deterministic Büchi automata and weak deterministic Büchi automata.
- EPMC

EPMC is a model checker for probabilistic models. It is a successor of the model checker IscasMC which only focused on PLTL model checking over MDP. EPMC supports Markov chains and Markov decision Processes (MDP), and properties specified in PCTL, PLTL and their combination PCTL*, as well as PETL for epistemic properties. It implements the efficient algorithm in particularly tuned to handle linear time properties. The main characteristics of EPMC are the high modularity of the tool, the possibility to extend EPMC with plugins to add new functionalities, and its availability on multiple platforms. EPMC achieves its flexibility by an infrastructure that consists of a minimal core part and multiple plugins that is very convenient to develop a new model checker based on the core parts of EPMC.
- PyBDR
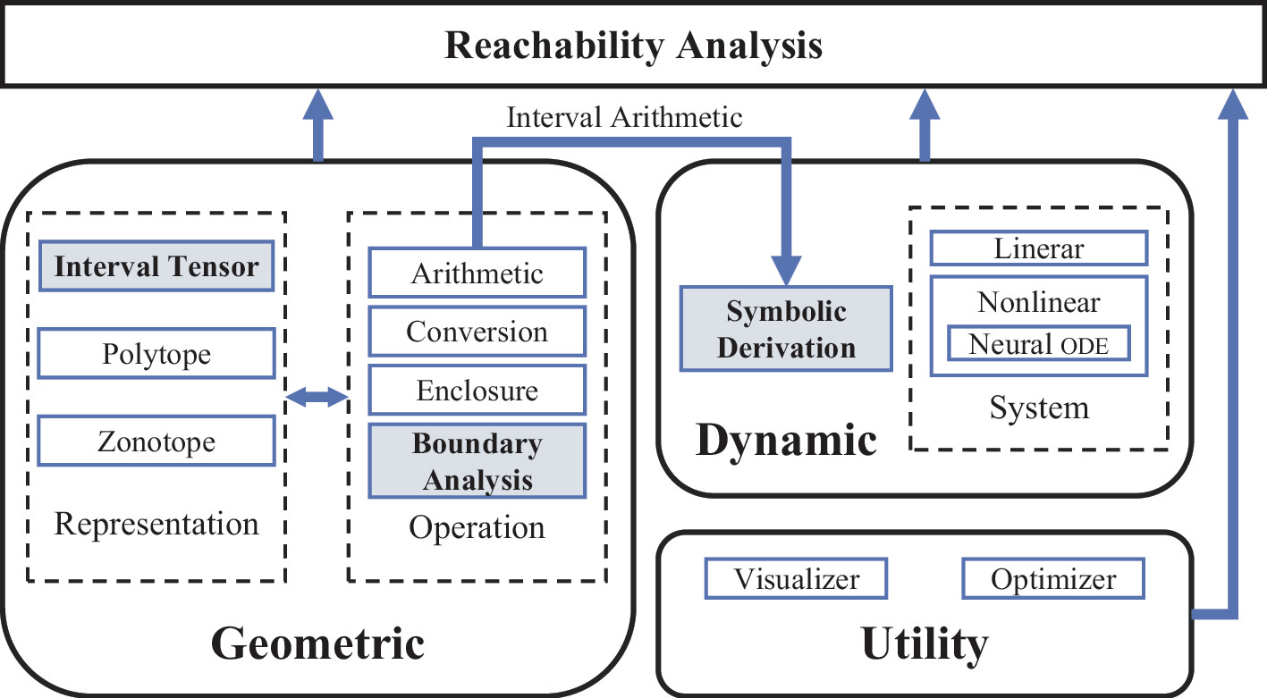
PyBDR is a Python reachability analysis toolkit based on set-boundary analysis, which centralizes on widely-adopted set propagation techniques for formal verification, controller synthesis, state estimation, etc. It employs boundary analysis of initial sets to mitigate the wrapping effect during computations, thus improving the performance of reachability analysis algorithms without significantly increasing computational costs.
- PacPMA
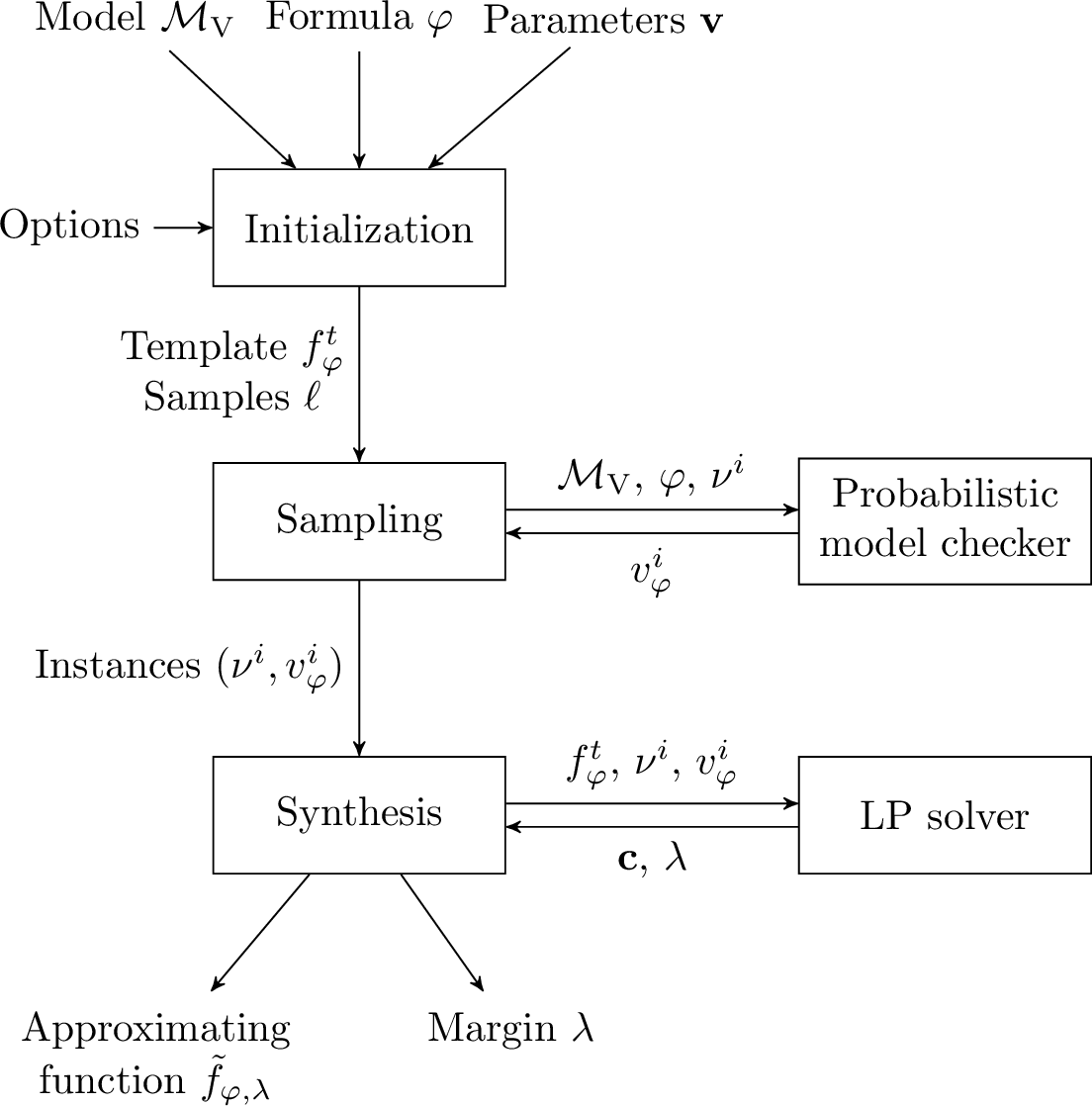
PacPMA is a command line tool written in JAVA. It implements algorithms for synthesizing polynomials to approximate the rational functions according to the scenario approach for parametric probabilistic model checking.
To perform such a synthesis, PacPMA delegates several of the underlying tasks to specialized tools, such as STORM and MATLAB.